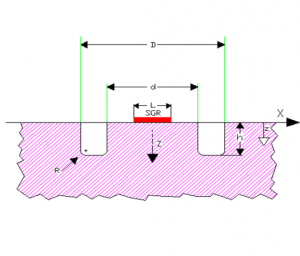
Bei der Ringkern-Methode wird ein Schlitz um eine spezielle DMS-Rosette mit 3 überlappenden Gittern mit Hilfe eines speziellen Elektromotors zum Bohren hergestellt. Der Bohrvorgang wird mit aufeinanderfolgenden Tiefenschritten durchgeführt: Am Ende jedes Bohrschritts werden die entspannten Dehnungen durch einen speziellen digitalen DMS-Verstärker erfasst. Nachdem alle Dehnungskurven erfasst wurden, werden diese verarbeitet, um die ursprünglich im Bauteil vorhandene Eigenspannung zu bewerten.

Die Größe des Schlitzes beträgt ca. 18 mm x 14 mm (Außen- und Innendurchmesser) mit einer typischen Tiefe von 4 bis 5 mm. Die Methode ermöglicht auch die Berechnung von gleichmäßigen und ungleichmäßigen Eigenspannungen in der zu untersuchenden Dicke.

Diese Art der Messung hat eine Reihe von bedeutenden Vorteilen gegenüber anderen Techniken, die Dehnungsmessstreifen zur Messung von Eigenspannungen verwenden: Erstens erzeugt die Ringkern-Methode bei gleichem Eigenspannungsbereich ein größeres Dehnungssignal (ca. 3-4 mal größer als die Sackloch-Methode) und garantiert aus diesem Grund eine größere Genauigkeit bei der Dehnungsmessung. Darüber hinaus hat die Methode eine geringere Empfindlichkeit gegenüber Exzentrizitätsfehlern.

Die Ringkern-Dehnungsmessstreifen-Methode ist noch nicht weltweit genormt; es gibt jedoch mehrere anerkannte Verfahren für spezifische industrielle Anwendungen (z. B. die KWU-Methode) zur Bewertung von Eigenspannungen (hauptsächlich an großen Schmiedeteilen). Bei diesen Bauteilen ändert das Vorhandensein eines kleinen Schlitzes auf der Oberfläche des Teils (der später durch Bearbeitung entfernt werden kann oder nicht) nichts an der Integrität und Funktionalität des mechanischen Teils.